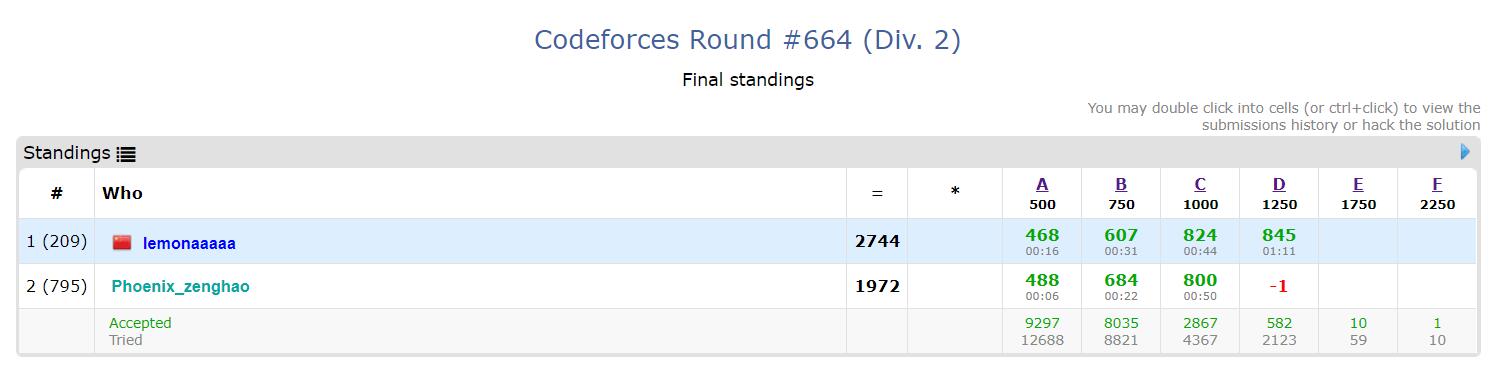
A. Boboniu Likes to Color Balls
题目链接
题目原文
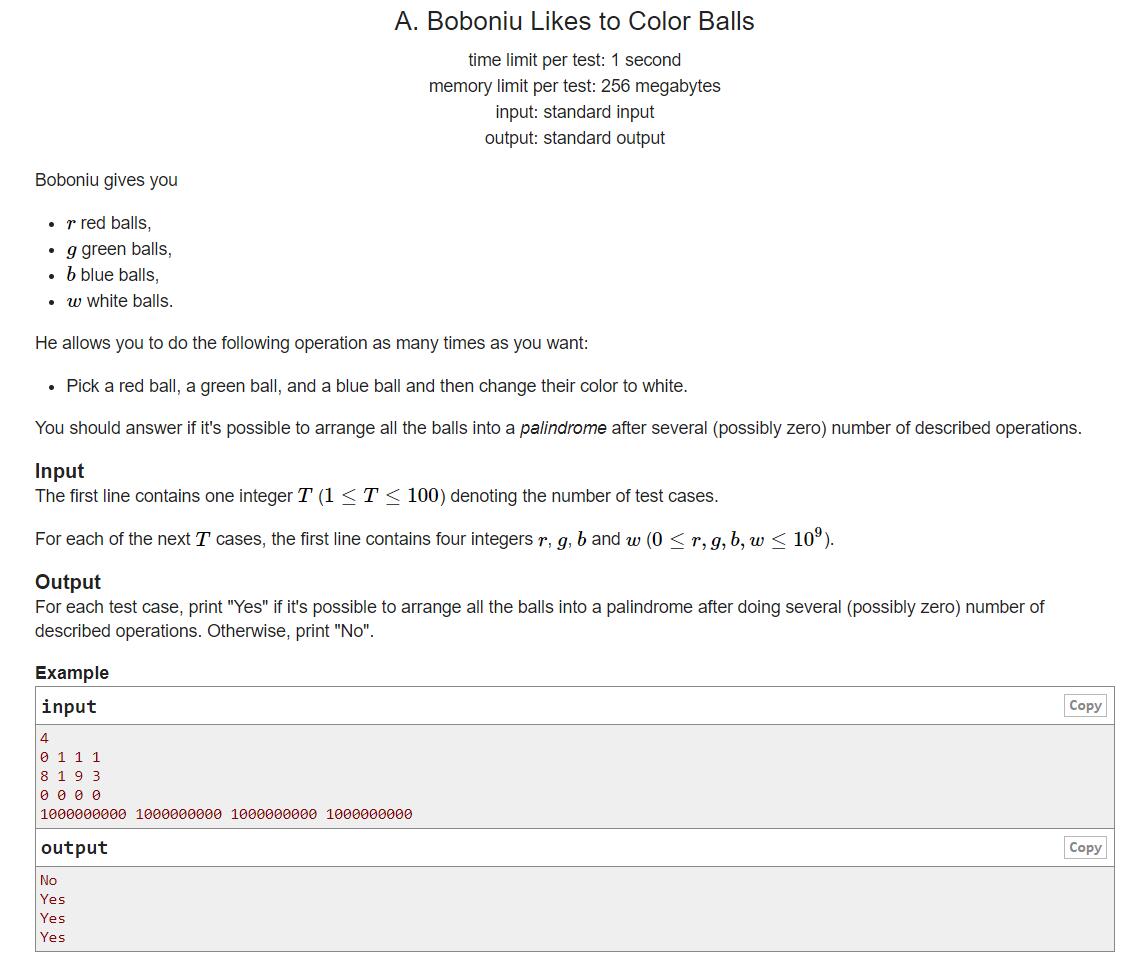
题目大意
给出红球的数量,绿球的数量,蓝球的数量,白球的数量,并且你有一次机会将一个红球、一个绿球和一个蓝球都涂成白球。询问是否可能用这些球组成回文串。
解题思路
四种球中如果最多只有一种球为奇数,那么一定可以组成回文串(将奇数个的那种球放最中间)。另外要注意当红球、蓝球、绿球的数量都大于0才能都涂成白球(白球数量要记得+=3)。
解法
如上。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=200005;
long long T,r,g,b,w;
long long get(long long x) {if(x&1) return 1;return 0;}
int main()
{
#ifdef lemon
freopen("A.txt","r",stdin);
#endif
scanf("%lld",&T);
while(T--)
{
scanf("%lld%lld%lld%lld",&r,&g,&b,&w);
bool flag=false;
long long temp=get(r)+get(g)+get(b)+get(w);
if(temp<=1) flag=true;
if(r&&g&&b) r--,g--,b--,w+=3;
temp=get(r)+get(g)+get(b)+get(w);
if(temp<=1) flag=true;
if(flag) printf("YES\n");
else printf("NO\n");
}
return 0;
}
|
B. Boboniu Plays Chess
题目链接
题目原文

题目大意
在一个n×m的棋盘上,位置(Sx,Sy)上有一个车(只能走直线)。求一种走法遍历整个棋盘。
解题思路
因为题目没有限制每个点只能走一次,那就随意走就好了。为了方便我采用的是一行一行地走,碰到边界拐弯。
解法
如上。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=200005;
int ansx[maxn],ansy[maxn],n,m,sx,sy;
bool vis[105][105];
int main()
{
#ifdef lemon
freopen("B.txt","r",stdin);
#endif
scanf("%d%d%d%d",&n,&m,&sx,&sy);
int now=1;
ansx[now]=sx;ansy[now]=sy;
vis[sx][sy]=true;
for(int i=1;i<=m;i++)
{
if(vis[sx][i]) continue;
ansx[++now]=sx;ansy[now]=i;
}
int cnt=1;
for(int i=sx+1;i<=n;i++)
{
if(cnt&1)
{
for(int j=m;j;j--)
{
ansx[++now]=i;ansy[now]=j;
}
}
else
{
for(int j=1;j<=m;j++)
{
ansx[++now]=i;ansy[now]=j;
}
}
cnt++;
}
for(int i=sx-1;i;i--)
{
if(cnt&1)
{
for(int j=m;j;j--)
{
ansx[++now]=i;ansy[now]=j;
}
}
else
{
for(int j=1;j<=m;j++)
{
ansx[++now]=i;ansy[now]=j;
}
}
cnt++;
}
for(int i=1;i<=now;i++) printf("%d %d\n",ansx[i],ansy[i]);
return 0;
}
|
C. Boboniu and Bit Operations
题目链接
题目原文

题目大意
给出一个长度为n的a数组和一个长度为m的b数组,对于a数组中每一个元素ai,在b数组里面找到一个元素与它求按位与,得到ci,求c1∣c2∣…∣cn的最小值。
解题思路
因为ai,bi的范围很小,而或起来值不会超过maxmaxai,maxbj,所以我们直接从小到大枚举答案进行验证就好。时间复杂度O(n⋅m⋅29)
解法
枚举答案,对于每一个答案ans,判断是否存在aiandbj是ans的子集。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=200005;
int n,m,a[maxn],b[maxn];
int main()
{
#ifdef lemon
freopen("C.txt","r",stdin);
#endif
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]);
for(int ans=0;ans<(1<<9);ans++)
{
bool flag=true;
for(int i=1;i<=n;i++)
{
bool f=false;
for(int j=1;j<=m;j++)
{
if((a[i]&b[j]&ans)==(a[i]&b[j])) f=true;
}
if(!f)
{
flag=false;
break;
}
}
if(flag)
{
printf("%d\n",ans);
break;
}
}
return 0;
}
|
D. Boboniu Chats with Du
题目链接
题目原文

题目大意
给出n个值a1,a2,a3…an,每天你可以选择一个值(不能重复选),如果这个值大于了m,那么你在接下来d天内不能选择。现在一共有n天,求最后能得到的最大的值的和。
解题思路
朴素解法:
这明显是一个01背包,如果ai小于等于m,那么cost就为1;否则cost就为d+1。直接做01背包,然后你就会发现TLE了。
解法:
因为d是固定的,所以如果我们要选ai大于m的值,一定从最大的开始选,选ai小于等于m的值同理。所以我们排序后对这两部分分别做前缀和,然后我们再直接暴力枚举选多少个ai小于等于m的值,然后由于d是固定的,所以我们可以O(1)算出可以选多少个ai大于m的值,用前缀和O(1)更新答案。总复杂度O(n⋅logn)。
另外注意边界,同学pretest AC了,一觉醒来就WA了。
解法
前缀和+枚举
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=200005;
long long n,d,m,a[maxn],f[maxn][2],s[maxn],ans=0;
int main()
{
#ifdef lemon
freopen("D.txt","r",stdin);
#endif
scanf("%lld%lld%lld",&n,&d,&m);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
sort(a+1,a+n+1);
int tot=0;
for(int i=1;i<=n;i++)
{
if(a[i]<=m) tot++;
}
for(int i=tot;i;i--) s[i]=s[i+1]+a[i];
for(int i=n;i>=tot+1;i--) s[i]=s[i+1]+a[i];
for(int i=0;i<=tot;i++)
{
int tim=(n-i+d)/(d+1);
if(n-tot<tim) continue;
int t1=tot-i+1;
if(t1>tot) t1=0;
int t2=n-tim+1;
ans=max(ans,s[t1]+s[t2]);
}
printf("%lld\n",ans);
return 0;
}
|