A. Suborrays

题目链接

题目原文

1391A

题目大意

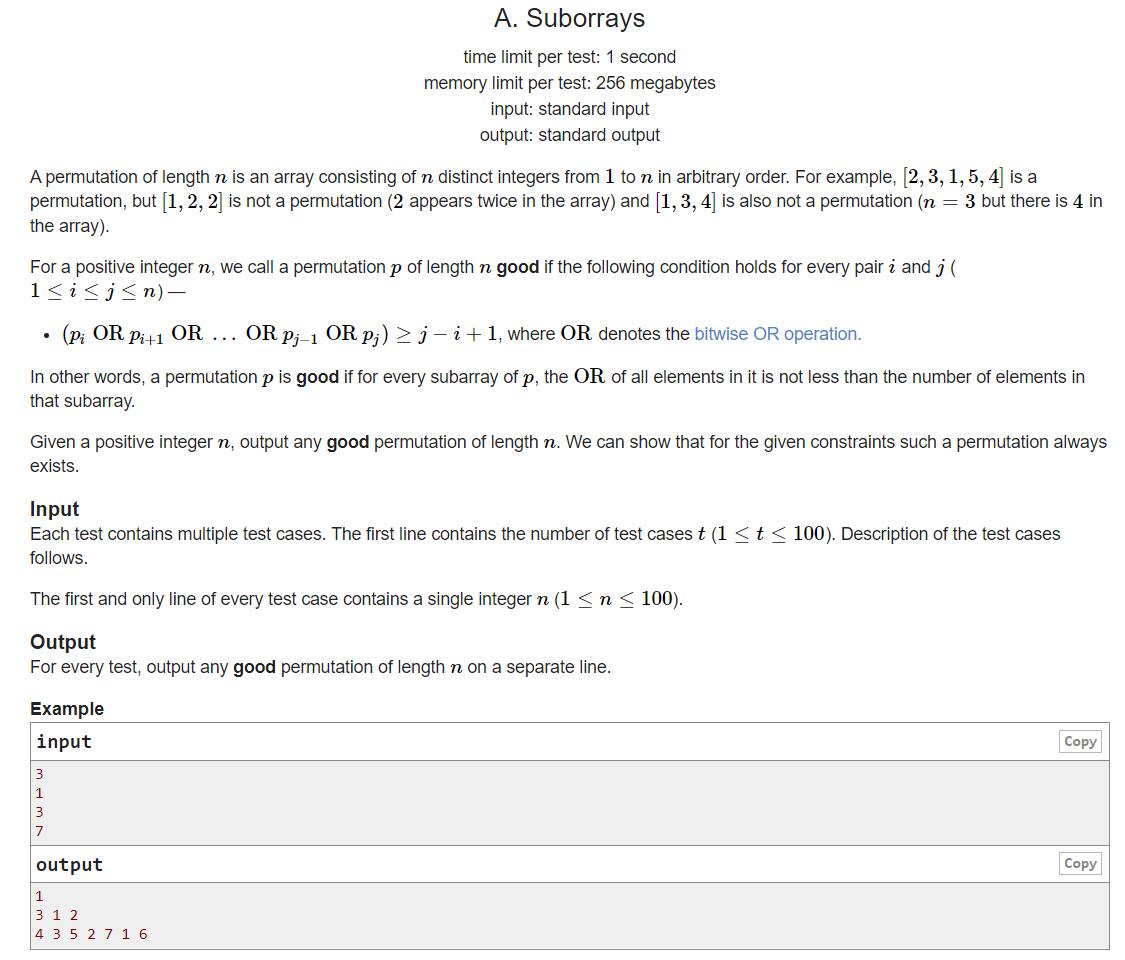
如果存在一个排列，对于其任意的连续子序列pi…pjp_i \dots p_j都满足pi  OR  pi+1  OR  …  OR  pj⩾j−i+1p_i \;OR \;p_{i+1} \;OR \;\dots \;OR \;p_j \geqslant j-i+1，则称这个排列为好排列。现在请输出任意长度为n的好排列。

解题思路

显然直接按从小到大输出一定能满足要求

解法

直接输出1  2  3  4  …  n1 \; 2 \; 3 \; 4 \; \dots \; n

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=200005;
int T,n,a[maxn];
int main()
{
 	#ifdef lemon
	freopen("A.txt","r",stdin);
	#endif
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++) printf("%d ",i);
/*		for(int i=1;i<=n;i++)
		{
			for(int j=i;j<=n;j++)
			{
				int temp=0;
				for(int p=i;p<=j;p++) temp|=p;
				if(temp<j-i+1) printf("NO\n");
			}
		}*/
		printf("\n");
	}
	return 0;
}

B. Fix You

题目链接

题目原文

1391B

题目大意

给出n行m列的矩阵，每个格子的值是’R’或者’D’。当移动到一个值为’R’的格子，那么会自动向右移动一格；当移动到一个值为’D’的格子，那么会自动向下移动一格。求至少修改多少个格子的值，能够满足“无论起始位置在哪，中途不能移动到边界外，并且最终都能到达最右下角的格子。

解题思路

我们发现’R’和’D’都是单调的，也就是说不会往回走，大体上的趋势一定是向右下角走的，我们只需要考虑是否会移出边界。

  • 判断第n行每一列的值是否为’R’，如果不是，则必须修改，否则会移出边界。
  • 判断第m列每一列的值是否为’D’，如果不是，则必须修改，否则会移出边界。

解法

答案即为第n行格子值为’D’的数量和第m列格子值为’R’的数量之和。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=200005;
int T,n,m,a[105][105];
char str[maxn];
int main()
{
 	#ifdef lemon
	freopen("B.txt","r",stdin);
	#endif
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++)
		{
			scanf("%s",str+1);
			for(int j=1;j<=m;j++)
				if(str[j]=='R') a[i][j]=0;
				else a[i][j]=1; 
		}
		int ans=0;
		for(int i=1;i<=n-1;i++) if(!a[i][m]) ans++;
		for(int i=1;i<=m-1;i++) if(a[n][i]) ans++;
		printf("%d\n",ans);
	}
	return 0;
}

C. Cyclic Permutations

题目链接

题目原文

1391C

题目大意

语言表达能力比较差，叙述上存在困难，直接看原文吧……那两个条件就是与最近的大于它的下标连边。

解题思路

考虑i<j<ki<j<k，那么我们发现只有ai>aj<aka_i>a_j<a_k能够构成简单环（此时ii与jj连边，jj与kk连边，ii与kk连边）。因为题目只需要满足存在一个简单环就行了，那就是只需要存在一个子序列（不一定连续）满足这个条件的就可以。

最开始尝试去用排列组合的方法直接算，后来发现比较困难，有重复情况。然后后来想到可以用总方案数-不满足要求的方案数。

显然总方案数为n!，那么现在考虑不满足要求的方案数。前面说到只要存在一个小的在中间，两边存在两个比它大的就行。那么我们就考虑最大的数，也就是n的位置。

  • 将n放第1个位置，左边放0个数，右边放n-1个数，且顺序必须是从大到小，所以方案数为C(n-1,0)
  • 将n放第2个位置，左边放1个数（从n-1个数中选1个），右边放n-2个数，且两边顺序必须是从n的位置开始，向两边从大到小排列（合唱队形），所以方案数为C(n-1,1)
  • 将n放第3个位置，左边放2个数（从n-1个数中选2个），右边放n-3个数，且两边顺序必须是从n的位置开始，向两边从大到小排列（合唱队形），所以方案数为C(n-1,2)
  • 将n放第n个位置，左边放n-1个数（从n-1个数中选n-1个），右边放0个数，且两边顺序必须是从n的位置开始，向两边从大到小排列（合唱队形），所以方案数为C(n-1,n-1)

所以不合法的方案数为∑i=0n−1(n−1i)=2n−1\sum\limits_{i=0}^{n-1}\dbinom{n-1}{i} = 2^{n-1}

解法

答案即为n!−2n−1n!-2^{n-1}

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1000005;
const long long mod=1e9+7;
long long fac[maxn];
long long poww(long long x,long long k)
{
	long long ans=1;
	while(k)
	{
		if(k&1) ans=(ans*x)%mod;
		x=(x*x)%mod;
		k>>=1;
	}
	return ans;
}
int main()
{
 	#ifdef lemon
	freopen("C.txt","r",stdin);
	#endif
	long long n;
	scanf("%lld",&n);
	long long ans=0;
	fac[0]=fac[1]=1;
	for(long long i=2;i<=n;i++) fac[i]=(fac[i-1]*i)%mod;
	ans=fac[n];
	ans=ans-poww(2ll,n-1);
	ans=(ans%mod+mod)%mod;
	printf("%lld\n",ans);
	return 0;
}

D. 505

题目链接

题目原文

1391D

题目大意

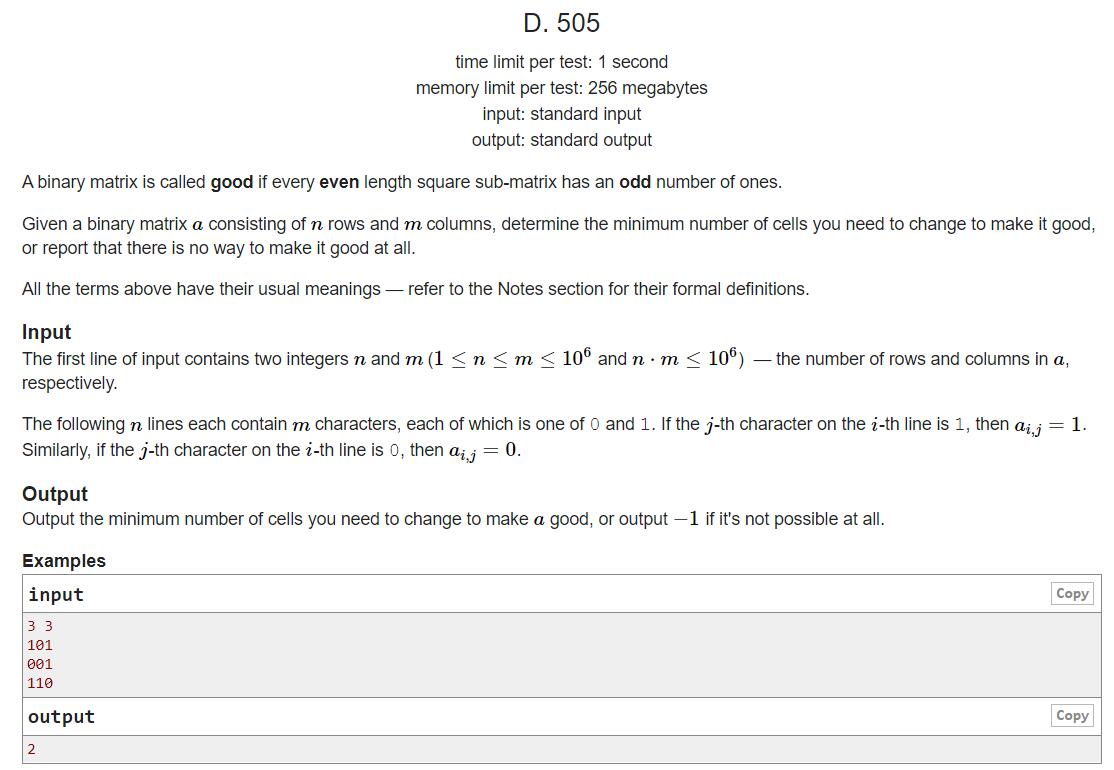
如果一个二进制矩阵是good的，那么它的所有边长为偶数的子矩阵中1的个数都是奇数个。
给出n行m列的矩阵，求修改多少次矩阵中的值能够使这个矩阵变为good的。如果不存在修改方案满足要求，输出-1。

解题思路

如果n=1||m=1，那么没有边长为偶数的子矩阵，输出0
如果n>=4&&m>=4，那么考虑两个连续的2x2的矩阵。如果这两个连续的2x2矩阵都满足要求，也就是说这两个连续的矩阵中1的个数都是奇数，那么这两个矩阵合起来的2x4的矩阵中1的个数就为偶数了。所以n>=4&&m>=4一定不存在合法的矩阵，也就是无论怎么修改都不能满足要求，所以输出-1

现在n就只能是2或3了，考虑动态规划。f[i][j]表示第i列的状态为j，j为3位二进制，表示这一列的3位分别为0或者1。那么我们可以枚举这一列的状态和上一列的状态进行转移。
假设这一列原来的状态是now（输入的状态），枚举的状态是j，上一列的状态是p。如果j和p满足要求，那么我们就可以进行转移，而满足的要求为这相邻的两列所有长度为偶数的子矩阵的1的个数为奇数，这里预处理一下就好（最大也就是3x2的矩阵）。

解法

转移方程f[i][j]=min(f[i][j],f[i-1][p]+(now^j)中1的个数);
now^j中1的个数即为需要修改这一列的数的个数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
using namespace std;
const int maxn=1000005;
int n,m,ans=0x7f7f7f7f;
int a[4][maxn],f[maxn][8];
bool ok[8][8]={false};
int calc(int x)
{
	int ans=0;
	while(x)
	{
		if(x&1) ans++;
		x>>=1;
	}
	return ans;
}
int main()
{
 	#ifdef lemon
//	freopen("D.txt","r",stdin);
	#endif
	scanf("%d%d",&n,&m);
	if(n>=4&&m>=4) return printf("-1\n"),0;
	if(n==1||m==1) return printf("0\n"),0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++) scanf("%1d",&a[i][j]);
	for(int i=0;i<8;i++)
	{
		for(int j=0;j<8;j++)
		{
			int t[3];
			t[0]=t[1]=t[2]=0;
			for(int p=0;p<n;p++)
			{
				if((1<<p)&i) t[p]++;
				if((1<<p)&j) t[p]++;
			}
			bool flag=true;
			for(int p=0;p<n-1;p++)
			{
				if(!((t[p]+t[p+1])&1)) flag=false;
			}
			if(flag) ok[i][j]=true;
		}
	}
	memset(f,0x7f7f7f7f,sizeof(f));
	for(int i=0;i<8;i++) f[0][i]=0;
	for(int i=1;i<=m;i++)
	{
		int now=a[1][i]+a[2][i]*2+a[3][i]*4;
		for(int j=0;j<8;j++)
		{
			for(int p=0;p<8;p++)
			{
				if(!ok[j][p]) continue;
				f[i][j]=min(f[i][j],f[i-1][p]+calc(now^j));
			}
		}
	}
	for(int i=0;i<8;i++) ans=min(ans,f[m][i]);
	printf("%d\n",ans);
	return 0;
}

round-663