A - Personalized Cup

Codeforces Round #522 (Div. 2, based on Technocup 2019 Elimination Round 3)

还没做，待补。

B - Playing Piano

Codeforces Round #522 (Div. 2, based on Technocup 2019 Elimination Round 3)

题目大意

给定一组序列a[i]，求一组序列b[i]，b[i]满足b[i]的数值不超过5，且如果a[i] < a[i+1]则b[i] < b[i+1]，如果a[i] > a[i+1]则b[i] > b[i+1]，如果a[i]=a[i+1]则b[i]!=b[i+1]，如果不存在这样的b[i]序列，则输出-1。

思路

记忆化搜索。不知道不加记忆化能不能过。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include&#60; cstdio &#62;
#include&#60; cstring &#62;
#include&#60; algorithm &#62;
using namespace std;
const int maxn=400005;
int n,a[maxn],ans[maxn],temp[maxn];
int f[maxn][6];
bool flag=false;
bool dfs(int x,int last)
{
	if(flag) return true;
	if(x==n+1)
	{
		flag=true;
		for(int i=1;i<=n;i++) ans[i]=temp[i];
		return true;
	}
	if(x==1)
	{
		for(int i=1;i<=5;i++)
		{
			if(!f[x+1][i]) continue;
			temp[x]=i;
			f[x+1][i]=dfs(x+1,i);
			if(flag) return true;
		}
	}
	else
	{
		if(a[x]>a[x-1])
		{
			for(int i=last+1;i<=5;i++)
			{
				if(!f[x+1][i]) continue;
				temp[x]=i;
				f[x+1][i]=dfs(x+1,i);
				if(flag) return true;
			}
		}
		else if(a[x]<a[x-1])
		{
			for(int i=1;i<last;i++)
			{
				if(!f[x+1][i]) continue;
				temp[x]=i;
				f[x+1][i]=dfs(x+1,i);
				if(flag) return true;
			}
		}
		else if(a[x]==a[x-1])
		{
			for(int i=1;i<=5;i++)
			{
				if(i==last) continue;
				if(!f[x+1][i]) continue;
				temp[x]=i;
				f[x+1][i]=dfs(x+1,i);
				if(flag) return true;
			}
		}
	}
	return false;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	memset(f,-1,sizeof(f));
	dfs(1,0);
	if(!flag) return printf("-1\n"),0;
	for(int i=1;i<=n;i++) printf("%d ",ans[i]);
	return 0;
}

C - A Prank

Codeforces Round #520 (Div. 2)

题目大意

有保证递增的n个数组成的序列

a1,  a2,  ...  ,  an  (1≤a1<a2<...<an≤1000)a_1,\;a_2,\;...\;,\;a_n\;(1\leq a_1<a_2<...<a_n\leq1000)

现在要抹去连续的几个数，求最长能抹去多少个数，能根据剩下的数推断出原序列。

思路

显然，如果能找回来，那么删去的数的值是连续的。直接找出值连续的序列的最长长度，注意因为值是大于0小于等于1000的，所以如果最后一个数是1000或者第一个数是1，是可以删去的。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include&#60; cstdio &#62;
#include&#60; cstring &#62;
#include&#60; algorithm &#62;
using namespace std;
const int maxn=100005;
int n,a[maxn],ans=0;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	a[0]=0;a[n+1]=1001;
	for(int i=1;i<=n+1;i++)
	{
		if(a[i]==a[i-1]+1)
		{
			int temp=0;
			while(a[i]==a[i-1]+1) i++,temp++;
			ans=max(ans,temp);
		}
	}
	ans=max(ans,1);
	printf("%d\n",ans-1);
	return 0;
}

D - Fun with Integers

Codeforces Round #520 (Div. 2)

题目大意

给你一个正整数n，(2≤n≤100000)，选一个数a，(2≤∣a∣≤n)，每次再选一个整数b，(2≤∣b∣≤n)，并且使得存在整数x，满足1 < ∣x∣且(a⋅x=b或b⋅x=a)，a就可以转换为b，并且获得∣x∣的分数，但是之后就不能使用a转换为b或b再转换为a的操作了，求得到分数的最大值。

思路

枚举所有成k倍数的a，b，答案就是k*4的和。
为什么呢？
以一对正整数a，b (a < b)为例：

a×k=ba×(−k)=−b(−a)×k=−b(−a)×(−k)=ba\times k=b\\a\times(-k)=-b\\(-a)\times k=-b\\(-a)\times(-k)=b

答案就很显然了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include&#60; cstdio &#62;
#include&#60; cstring &#62;
#include&#60; algorithm &#62;
using namespace std;
const int maxn=200005;
int n;
long long ans=0;
int main()
{
	scanf("%d",&n);
	for(int i=2;i<=n;i++)
	{
		for(int j=2;i*j<=n;j++)
		{
			ans+=j*4;
		}
	}
	printf("%lld\n",ans);
	return 0;
}

E - Banh-mi

Codeforces Round #520 (Div. 2)

题目大意

给出一个长度为n的01串。
每次可以选择获得并删除一个位置位置上的值 x，并且会使其他位置的值加上 x 。现在给出m个询问，每个询问是一个区间[l , r] ,在这个范围内能获得的最大价值是多少。

思路

如果我们先删去值为0的位置，那么对于其他位置的贡献始终为0，显然是最差解。
所以我们每次删去所有值中最大的值，这样就能保证其他位置全部加上这个最大的值，也就保证了答案最优。
用快速幂计算等比数列即可（做这道题的时候等比数列的公式我都忘了2333）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include&#60; cstdio &#62;
#include&#60; cstring &#62;
#include&#60; algorithm &#62;
#define lowbit(x) (x&(-x))
using namespace std;
const int maxn=200005;
const long long mod=1e9+7;
int n,a[maxn],c[maxn],q;
void add(int x,int v) {for(int i=x;i<=n;i+=lowbit(i)) c[i]+=v;}
int get(int x) {int t=0;for(int i=x;i;i-=lowbit(i)) t+=c[i];return t;}
long long poww(long long x,long long k)
{
	long long temp=1;
	while(k)
	{
		if(k&1) temp=(temp*x)%mod;
		x=(x*x)%mod;
		k>>=1;
	}
	return temp;
}
int main()
{
	scanf("%d%d",&n,&q);
	for(int i=1;i<=n;i++) scanf("%1d",&a[i]);
	for(int i=1;i<=n;i++) add(i,a[i]);
	while(q--)
	{
		int l,r;
		scanf("%d%d",&l,&r);
		long long sum=get(r)-get(l-1);
//		printf("$$%d\n",sum);
		long long zero=r-l+1-sum;
		long long s=poww(2ll,zero);
//		printf("**%lld\n",zero);
		long long ans=-(1-poww(2,sum));
//		printf("@@%lld\n",ans);
		ans=ans*s;
		ans%=mod;
		printf("%lld\n",ans);
	}
	return 0;
}

F - Barcelonian Distance

Codeforces Round #522 (Div. 2, based on Technocup 2019 Elimination Round 3)

题目大意

给出一条二维平面上的直线和两个点A、B，问从A点走到B点的最短路径长度。
点只能在给定直线和与坐标轴平行的直线上行走。

思路

CF1079D_sol

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include&#60; cstdio &#62;
#include&#60; cstring &#62;
#include&#60; algorithm &#62;
#include&#60; cmath &#62;
using namespace std;
const int maxn=200005;
double a,b,c,sx,sy,tx,ty;
double dis(double x,double y,double xx,double yy)
{
	return sqrt((xx-x)*(xx-x)+(yy-y)*(yy-y));
}
int main()
{
	scanf("%lf%lf%lf%lf%lf%lf%lf",&a,&b,&c,&sx,&sy,&tx,&ty);
	double lsx=-(b*sy+c)/a;
	double lsy=-(a*sx+c)/b;
	double ltx=-(b*ty+c)/a;
	double lty=-(a*tx+c)/b;
	double ans=fabs(tx-sx)+fabs(ty-sy);
	ans=min(ans,fabs(lsy-sy)+dis(sx,lsy,tx,lty)+fabs(lty-ty));
	ans=min(ans,fabs(lsy-sy)+dis(sx,lsy,ltx,ty)+fabs(ltx-tx));
	ans=min(ans,fabs(lsx-sx)+dis(lsx,sy,tx,lty)+fabs(lty-ty));
	ans=min(ans,fabs(lsx-sx)+dis(lsx,sy,ltx,ty)+fabs(ltx-tx));
	printf("%.10lf\n",ans);
	return 0;
}

G - Diverse Substring

Codeforces Round #522 (Div. 2, based on Technocup 2019 Elimination Round 3)

题目大意

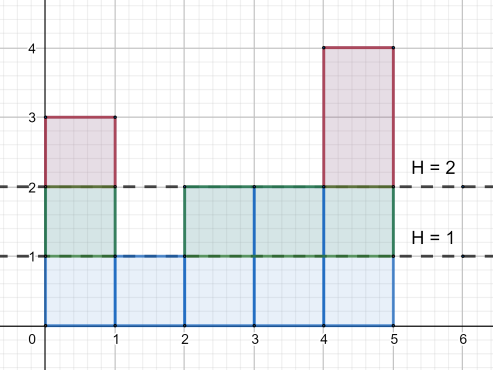
国王邀请k个人来赴宴就餐，每个人都吃了好几道菜（菜的数量对每个人来说都一样），每道菜都配有一套新的厨具。每一套器具都是一样的，由不同类型的器具组成，所有种类的器皿都由1到100编号。每一类器具最多在一道菜只能出现一次。晚餐结束后，客人们都被打发走了，国王想知道能多少餐具被偷。不幸的是，国王忘记了每一位客人有多少菜，但他知道晚餐后剩下的所有餐具的清单。求出丢失餐具的最小数量。

思路

找出个数最多的餐具数量maxx，因为每个人的餐具数量是相同的，所以maxx应该能被k整除，如果不能整除，说明一定存在拿走了的情况，题目又要保证丢失餐具数量最少，所以maxx取比最初maxx大且是k的倍数的值。那么maxx*餐具种类type就是最小的总数量，再减去剩下n个餐具得到的就是被偷走的餐具数量。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include&#60; cstdio &#62;
#include&#60; cstring &#62;
#include&#60; algorithm &#62;
#include&#60; cmath &#62;
using namespace std;
const int maxn=200005;
int n,k,cnt[maxn],maxx=0,types=0;
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1,x;i<=n;i++)
	{
		scanf("%d",&x);
		cnt[x]++;
	}
	for(int i=1;i<=100;i++)
	{
		if(!cnt[i]) continue;
		types++;
		maxx=max(cnt[i],maxx);
	}
	while(maxx%k) maxx++;
	printf("%d\n",maxx*types-n);
	return 0;
}

H - Math

Codeforces Round #520 (Div. 2)

题目大意

输入一个数，可以对这个数进行两种操作：

  1. 乘以任何一个数 x
  2. 如果这个数为平方数（4，9，16，25…），可以对这个数开根号。

求经过若干次操作后，这个数最小能变成哪个数？并输出最少的变换次数。

思路

  • 第一问：最小能变成哪个数就直接是所有质因数的乘积，这应该很好理解。
  • 第二问：如果所有的质因数的个数都是2的n次方，那么显然直接开n-1次根就好了。那如果不是以上情况怎么办呢？就再乘上一个数变成那样就好了，因为没有限制乘什么数，所以乘法一步到位是合法且最优的。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include&#60; cstdio &#62;
#include&#60; cstring &#62;
#include&#60; algorithm &#62;
#include&#60; cmath &#62;
using namespace std;
const int maxn=1000005;
int num[maxn],cnt=0,n,a[maxn],ans=1,maxx=0;
int main()
{
	scanf("%d",&n);
	for(int i=2;i<=n;i++)
	{
		if(n%i==0) num[++cnt]=i;
	}
	for(int i=1;i<=cnt;i++)
	{
		if(n&&n%num[i]==0) ans*=num[i];
		while(n&&n%num[i]==0)
		{
			a[i]++;
			n/=num[i];
			maxx=max(maxx,a[i]);
		}
		if(!n) break;
	}
	printf("%d ",ans);
	
	int tt=0;
	for(int i=0;i<=30;i++)
	{
		if((1<<i)>=maxx)
		{
			tt=i;
			break;
		}
	}
	bool f=false;
	for(int i=1;i<=cnt;i++)
	{
		if(!a[i]) continue;
		if(a[i]!=(1<<tt)) f=true;
	}
	if(f) tt++;
	printf("%d\n",tt);
	return 0;
}

总结

一切看起来不可做的题都有巧妙的解法。

rank