居然这场比赛是11点35开始，打完都2点了，开学第一天就这样，根本hold不住。
总体来说，这次稀奇古怪的想法比较多，所以作为新手刚入门，也过了3道，rating上了1500，比初始值高了……
另外这场比赛的USACO风格倍感亲切。

A. Cow and Haybales

题目链接

题目原文

1307A

题目大意

给从左到右 nn 个堆 ，每个堆有 aia_i 个东西，每天可以把第 ii 个堆里的 11 个东西拿到第 i−1i-1 个堆里。现问 dd 天后第一个堆里最多有多少个东西。

思路

直接模拟，第 ii 个堆里的一个东西搬到第一个堆里需要花费 i−1i-1天。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include < cstdio >
#include < cstring >
#include < algorithm >
using namespace std;
const int maxn=200005;
int T,n,d,a[maxn];
int main()
{
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&d);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		int ans=a[1];
		for(int i=2;i<=n;i++)
		{
			while(a[i]&&d>=i-1)
			{
				ans++;
				a[i]--;
				d-=(i-1);
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}

B. Cow and Friend

题目链接

题目原文

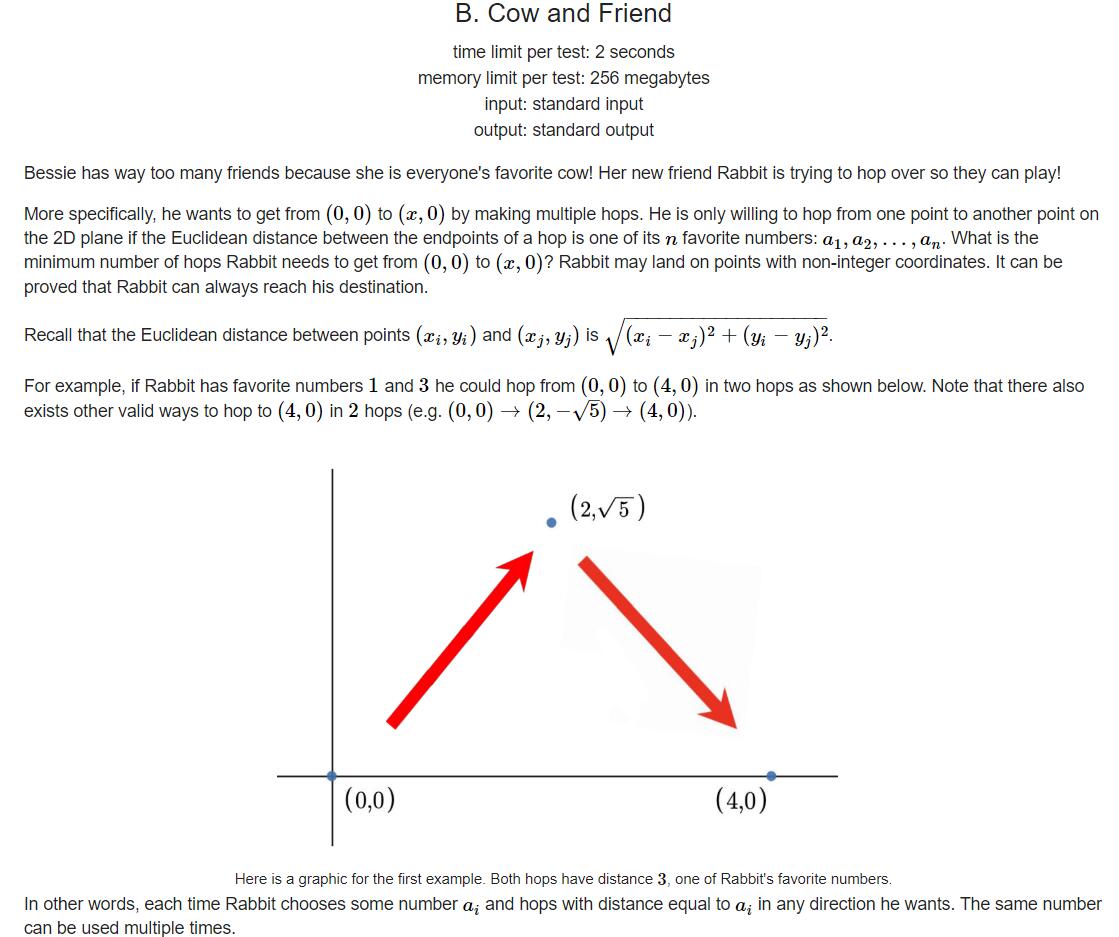
1307B

题目大意

给出 nn 个值和一个值 valval 。现在要从 (0,0)(0,0) 跳到 (val,0)(val,0) ，每次可以从 nn 个值中选一个来眺，求最少跳多少次可以到达。

思路

一般这种题都是找规律，就看能不能快速找到了（做了D题灵感才来）。
有以下几种情况：

  • 如果有刚好值为 valval 的，那么一次就跳到终点。
  • 如果有值大于 valval 的，那么两次就能跳到。因为可以第一次跳到垂直平分线 x=val2x=\frac{val}2 上。
  • 如果所有的值都小于都小于 valval ，那么最优的肯定是挑最大的值来跳，然后按照前两点相同的方式判断即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include &lt; cstdio &gt;
#include &lt; cstring &gt;
#include &lt; algorithm &gt;
using namespace std;
const int maxn=200005;
long long T,n,x,a[maxn];
bool cmp(int a,int b) {return a>b;}
int main()
{
	scanf("%lld",&T);
	while(T--)
	{
		scanf("%lld%lld",&n,&x);
		for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
		sort(a+1,a+n+1,cmp);
		long long ans=x/a[1];
		bool flag=false;
		if(x%a[1]) ans++;
		for(int i=1;i<=n;i++)
			if(a[i]==x)
			{
				ans=1;
				flag=true;
			}
		if(!flag&&a[1]>x) ans=2;
		printf("%lld\n",ans);
	}
	return 0;
}

C. Cow and Message

题目链接

题目原文

1307C

题目大意

求串 ss 中出现次数最多的子序列 tt 的出现次数。其中子序列在 ss 中所对应的下标必须构成等差数列。

思路

首先可以确定的是，我们找到的这个子序列，长度一定是 11 或者 22 ，因为如果大于 22 的话，条件就更难满足了。
那这道题也有三种情况：

  • tt 为单字符，那么答案即为该字符出现的次数。
  • tt 为双字符，且两个字符是相同的，计该字符出现的次数为 nn ，则答案为 n×(n−1)2\frac{n\times(n-1)}2 。
  • tt 为双字符，且两个字符不同。那我们枚举每两个不同的字符，再拿其中一个字符枚举一个断点，去统计这些断点做出的贡献和，不断更新即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include &lt; cstdio &gt;
#include &lt; cstring &gt;
#include &lt; algorithm &gt;
using namespace std;
const int maxn=200005;
char str[maxn];
long long alp[maxn][26],ans=0;
long long ss(long long x) {return (x-1)*x/2;}
int main()
{
	#ifdef lemon
//	freopen("C.in","r",stdin);
//	freopen("my.out","w",stdout);
	#endif
	scanf("%s",str+1);
	int n=strlen(str+1);
	for(int i=1;i<=n;i++) alp[i][str[i]-'a']++;
	for(int i=1;i<=n;i++)
		for(int j=0;j<26;j++)
			alp[i][j]+=alp[i-1][j];
	for(int i=0;i<26;i++)
	{
		for(int j=0;j<26;j++)
		{
			if(i==j) continue;
			long long temp=0;
			for(int p=1;p<=n;p++)
			{
				if(str[p]-'a'==i)
				{
					temp+=alp[n][j]-alp[p][j];
				}
			}
			ans=max(ans,temp);
		}
	}
	for(int i=0;i<26;i++) ans=max(ans,ss(alp[n][i]));
	for(int i=0;i<26;i++) ans=max(ans,alp[n][i]);
	printf("%lld\n",ans);
	return 0;
}

D. Cow and Fields

题目链接

题目原文

1307D

题目大意

给一个 nn 个点， mm 条边的无向图，边长都为 11 ，现在有 kk 个特殊点，现必须选择 kk 个特殊点中任意两个连上。求连上之后的 11 号点到 nn 号点距离的最小值最大。

思路

几百年没碰过图论了，但是建图还是知道怎么建的……
先正反各跑一遍bfs，求出起点和终点的单源最短路径。然后我们就要确定加哪两个点之间的边了。我直接贪心，想的是肯定要找距起点距离尽量相同的两个点，造成贡献的可能性更小。因为如果加一条边并不会导致最小值变大，只有可能变小或者不变，那么我们就尽量让它不变。就这样，过了样例交上去，就AC了……

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include &lt; cstdio &gt;
#include &lt; cstring &gt;
#include &lt; algorithm &gt;
#include &lt; queue &gt;
using namespace std;
const int maxn=400005;
struct node
{
	int to,next;
} edge[maxn<<1];
struct Node
{
	int x,val;
} b[maxn];
int head[maxn],k,n,m,cnt=0,dist[maxn],st[maxn],sp=0,bp=0,a[maxn],dist2[maxn];
bool spe[maxn],vis[maxn];
void add(int u,int v)
{
	edge[++cnt].to=v;
	edge[cnt].next=head[u];
	head[u]=cnt;
}
void bfs()
{
	queue<int> q;
	memset(dist,0x7f7f7f7f,sizeof(dist));
	q.push(1);vis[1]=true;dist[1]=0;
	if(spe[1])
	{
		b[++bp].x=1;
		b[bp].val=0;
	}
	while(!q.empty())
	{
		int x=q.front();q.pop();
		for(int i=head[x];i;i=edge[i].next)
		{
			dist[edge[i].to]=min(dist[edge[i].to],dist[x]+1);
			if(!vis[edge[i].to])
			{
				q.push(edge[i].to);
				vis[edge[i].to]=true;
				if(spe[edge[i].to])
				{
					b[++bp].x=edge[i].to;
					b[bp].val=dist[edge[i].to];
				}
			}
		}
	}
}

void bfs2()
{
	queue<int> q;
	memset(dist2,0x7f7f7f7f,sizeof(dist2));
	memset(vis,false,sizeof(vis));
	q.push(n);vis[n]=true;dist2[n]=0;
	while(!q.empty())
	{
		int x=q.front();q.pop();
		for(int i=head[x];i;i=edge[i].next)
		{
			dist2[edge[i].to]=min(dist2[edge[i].to],dist2[x]+1);
			if(!vis[edge[i].to])
			{
				q.push(edge[i].to);
				vis[edge[i].to]=true;
			}
		}
	}
}
/*void dfs(int x,int dis)
{
	vis[x]=true;
	for(int i=head[x];i;i=edge[i].next)
	{
		if(vis[edge[i].to]) continue;
		if(dist[edge[i].to]+1==dis)
		{
			if(spe[edge[i].to])
			{
				st[++sp]=edge[i].to;
				b[++bp].x=edge[i].to;
				b[bp].val=dist[edge[i].to];
			}
			dfs(edge[i].to,dis-1);
		}
	}
}*/
bool cmp(Node a,Node b) {return a.val<b.val;}
int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=k;i++)
	{
		scanf("%d",&a[i]);
		spe[a[i]]=true;
	}
	for(int i=1;i<=m;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);add(b,a);
	}
	bfs();
	bfs2();
/*	memset(vis,false,sizeof(vis));
	if(spe[n])
	{
		st[++sp]=n;
		b[++bp].x=n;
		b[bp].val=dist[n];
	}
	dfs(n,dist[n]);*/
	int ans=0;
	sort(b+1,b+bp+1,cmp);
	for(int i=1;i<bp;i++)
	{
		ans=max(ans,dist2[b[i+1].x]+1+dist[b[i].x]-dist[1]);
	}
	ans=min(ans,dist[n]);
	printf("%d\n",ans);
	return 0;
}

未完待续……（可能吧）

round-621